Why are the values of the initial modulus of elasticity of concrete during compression and tension multiplied by 10^-3? There must be a positive degree. It turns out that the modulus of elasticity for concrete B25 is 30 kPa, but it is equal to 30 GPa!
Because when compiling various kinds of tables, there is no need to write 3 additional zeros in each cell; it is enough to simply indicate that the table values are underestimated by 1000 times. Accordingly, in order to determine the calculated value, you need to not divide the table value, but multiply it by 1000. This practice is used in the preparation of many regulatory documents (this is the form in which the tables are given) and I see no reason to abandon it.
Then it turns out that the modulus of elasticity of the reinforcement must be divided by 10 to the fifth power. Or am I missing something? In recommendations for the calculation and design of solid floor slabs of large-panel buildings, 1989. and the concrete modulus and the reinforcement modulus are multiplied by 10 to the third and 10 to the fifth power, respectively
I'll try to explain again. Look carefully at Table 1. If in the title line instead of “Elasticity modulus E, MPa” I would write “Elasticity modulus E, MPa•10^-5”, then this would save me from the need to add to the value of the elasticity modulus in each line “•10^5”. But the values of elastic moduli for different materials differ hundreds and even thousands of times, so this form of notation for Table 1 is not entirely convenient. In tables 2 and 2.1, the values of the initial elastic moduli differ slightly and therefore this form of notation was used. Moreover, if you open these regulatory documents, you will see this for yourself. This tradition was formed in that distant time when there was no trace of a PC and a typesetter manually typed type into a printing press, so in this case all the questions are not for me, but for Gutenberg and his followers.
Perhaps the modulus of elasticity would be easier to remember and perceive in GPa, because then steel has approximately 200 units, and wood 10.12.
It’s quite possible, but GigaPascals are not the most visual and easy-to-understand dimension.
Note:
Perhaps your question, especially if it concerns structural calculations, will not appear in the general list or will remain unanswered, even if you ask it 20 times in a row. Why is explained in sufficient detail in the article “Make an appointment with a doctor” (link in the header of the site).
Modulus of elasticity of concrete (initial, deformation): B15, B20, B25, B30
Concrete building structures are constantly subject to heavy loads. This must be taken into account at the planning stage. Therefore, technologists have developed a system for giving concrete the ability to elastically deform under the influence of factors such as pressure and force. The value characterizing this indicator is called the elastic modulus of concrete.
When calculating a building structure, specialists use a formula to calculate the stress ratio and deformation modulus of B25 concrete or a material of another class. For convenience, the data obtained in the laboratory are entered into tables that comply with SNiP. They can always be used when designing any structure.
Definition of elasticity and units of measurement
The modulus value of any type of concrete is determined in accordance with the current SP 52-101-2003. This is a normative document, the tables of which contain all the necessary coefficients for determining the elasticity of a material per m2.
By performing special calculations taking into account the deformation of the material used, specialists can accurately determine the safety factor of an arched structure, any floor of a building, a road or railway bridge.
In the literature for professionals, the elasticity parameter is usually denoted by the letter E. Its value is influenced by the effective load and the structure of the concrete. The unit of measurement is the pascal, since the voltage caused in the prototype by the force acting on it is measured in pascals.
The elastic modulus of B20 and other types is influenced by production technology, in particular the method of hardening: natural, autoclave or heat treatment. The performance characteristics of the material play an important role.
Therefore, such an indicator as elasticity is not the same for one class. For example, if we consider cellular or heavy materials that have the same strength value per m2, then the values of their moduli will be different.
In order to increase the elastic modulus of B15 concrete, experts recommend using various methods for its production. Thus, during autoclave processing, higher elastic properties appear, reaching the number 17. By applying heat treatment using atmospheric pressure, the value can be increased to 20.5. The highest modulus value is achieved during natural hardening.
In a similar way, you can increase the elastic modulus of B25, the most popular among builders. It is important to remember that as the class indicator of a material increases, the indicator of its resistance to elastic deformation also increases.
Elastic modulus
Strictly speaking, the term “modulus of elasticity” (Young’s modulus) refers directly only to the straight-line portion of the stress-strain diagram or, in the absence of such a portion, to the tangent to the curve passing through the origin. This initial module has little practical value. It is possible to determine the elastic modulus from tangents passing through any point on the stress-strain graph, but this modulus is applicable only for very small load deviations above or below the level at which this modulus is determined. The magnitude of the observed deformations and the course of the stress-strain curve depend, at least in part, on the rate at which the load is applied. When the load is applied extremely quickly, for example in less than 0.01 sec, the strains are dramatically reduced and the curvature of the stress-strain relationship becomes extremely small. Increasing the loading time from 5 seconds to 2 minutes can change the deformation by 15%, but within the range of 2 to 10 minutes (and even up to 20), i.e., within the time usually used when testing samples on standard testing equipment, the increase There are negligible deformations. The increase in deformation under load, or part of such an increase, is due to the creep of concrete, but the separation of the elastic and plastic parts of the deformation is difficult due to the dependence of the instantaneous deformation on the loading rate. For practical purposes, the separation of deformations is carried out as follows: the deformation during loading is considered elastic, a further increase in deformation occurs due to the creep of concrete. The elastic modulus satisfying this condition is shown in Fig. 6.1 as the deformation modulus. There are currently no standard methods for determining the deformation modulus; in some laboratories it is determined at stress levels in the range from 28 to 140 kgf/cm2, in others - at stresses reaching 15, 25, 33 or 50% of the breaking load. Since the strain modulus decreases with increasing stress, the voltage at which it is determined must always be specified. This modulus is a static modulus of elasticity, since it is determined from the ratio of stress to strain, which, in contrast to the dynamic modulus, is set at 280 kgf/cm2. Determining the initial modulus of elasticity is associated with significant difficulties, but its approximate value can be determined indirectly: the secant to the stress-strain curve on the unloading branch is often, although not in all cases, parallel to the tangent passing through the origin. Repeated loading and unloading reduces creep, so the stress-strain diagram obtained after three or four loads has very little curvature. The influence of creep on the magnitude of the total deformation is significantly reduced when measuring deformations in a small range of stress variations, but in this case, accurate measurement of deformation is very difficult. The modulus of elasticity of concrete increases in proportion to the square root of its strength. This dependence is valid only for the main part of the graph and depends on the testing conditions of the samples: water-saturated samples are characterized by a higher elastic modulus than dry ones, while their strengths are at the same level. Aggregate properties also influence the elastic modulus of concrete; As the elastic modulus of coarse aggregate increases, the elastic modulus of concrete increases. The surface shape of the coarse aggregate and the characteristics of its surface can also influence the value of the elastic modulus of concrete and the type of graphical stress-strain relationship. Below is the modulus of elasticity of concrete of different strengths determined in accordance with the CP 2007-1960 guidelines for the design of prestressed concrete. The relationship between the elastic modulus and the strength of concrete also depends on the quantitative ratio of the components in the mixture (the elastic modulus of aggregates is usually higher than the elastic modulus of cement stone) and on the age of the samples: with increasing age of concrete, its elastic modulus increases faster than its strength. The relationship between the elastic modulus and the strength of concrete remains unchanged under the influence of elevated (up to 230 ° C) temperatures, since in this temperature range both the elastic modulus and the strength of concrete change with increasing temperature according to the same law. Issues related to the modulus of elasticity in compression were discussed above, however, for a number of concretes, the modulus of elasticity in tension has the same values as the modulus of elasticity in compression. The tensile modulus of elasticity can be determined from the results of bending tests of samples, and, if necessary, the results are adjusted for the effect of shear. In bending tests, the graphical stress-strain curve has a descending branch of the curve at loads close to failure, i.e. there is a decrease in stress, accompanied by an increase in concrete deformations. The same phenomenon is observed during compression tests, provided that the sample is loaded at a constant amount of deformation. The shear modulus of elasticity is not determined by direct experiments.
What does the elasticity of concrete depend on?
The main characteristic that determines the strength of concrete is its elasticity coefficient. It is important for professional designers who carry out calculations of the load capacities of concrete structures.
The factors affecting the magnitude of the module include the following:
- filler (its density directly affects the specific gravity of concrete; if it is gravel or crushed stone, the figure is higher);
- class (for example, in B10 the elasticity value is 19, and in B30 it is 32.5);
- age of the monolith (as this indicator increases, the strength of the concrete structure also increases).
The impact factor is the time during which the material is subjected to stress and air humidity. The moisture content of the environment affects such an indicator as the creep of concrete. In this case, the ambient temperature and the intensity of radioactive radiation are taken into account.
Such a characteristic as deformation largely depends on the presence of a metal frame used to reinforce the building structure. Metal has a much lower degree of destruction. Therefore, for structures that will regularly experience heavy loads, a spatial metal lattice is necessary.
There is a special table developed in accordance with the joint venture. It is used to determine the initial modulus of elasticity of concrete.
1.1.7. Concrete strain modulus
The initial modulus of elasticity of concrete under compression () corresponds only to elastic deformations that occur under instantaneous loading or under stresses. It is defined, in accordance with Hooke’s law, as the tangent of the angle of inclination of the straight line of elastic deformations to the abscissa axis (Fig. 16), i.e.:
(1.18)
where ρ = 1 MPa is the scale-size factor.
Rice. 16. Scheme for determining the deformation modulus of concrete:
1 – elastic deformations; 2 – secant; 3 – tangent; 4 – complete deformations
It is usually determined from special experiments on prisms at a low level of stress (), when concrete can be considered as an elastic material, or, if the cubic strength of concrete is known, then using various empirical formulas. So for heavy concrete of natural hardening
. (1.19)
The value during heat treatment of concrete is reduced by 10%, and with autoclave - by 25%.
When a load is applied to concrete, at which, at least for several minutes, due to the development of plastic deformations (including creep), the modulus of total concrete deformations becomes variable.
To calculate reinforced concrete structures, use the average modulus of deformation or the modulus of elastic-plasticity of concrete, which is the tangent of the angle of inclination of the secant drawn through the origin of coordinates and a point on the curve with a given stress, to the abscissa axis, i.e.
(1.20)
The relationship between and can be established by expressing according to (1.18) and (1.20) the same stress in concrete through elastic deformations and total deformations
(1.21)
where v = is the elastic-plasticity coefficient of concrete. The value of v during compression varies from 1 (during elastic operation of concrete) to 0.15 (at the moment preceding the destruction of concrete under very long loading).
The initial tensile modulus of elasticity of concrete in absolute value is taken equal to , i.e. , A
(1.22)
where vt = 0.15 is the value of the elastic-plasticity coefficient of concrete in tension at the moment preceding failure.
The values of concrete shear modulus G are taken according to the relationship established in the theory of elasticity
Substituting into it the initial coefficient of transverse deformation of concrete ν = 0.2, we obtain.
1.2. Reinforcement for reinforced concrete structures
1.2.1. Purpose of fittings and requirements for them
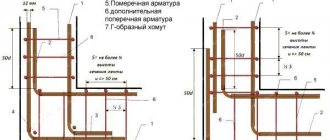
Reinforcement is understood as individual rods or entire frames, which are located in the mass of concrete in accordance with the static operating diagram of the structure.
Reinforcement in reinforced concrete structures is used primarily to absorb tensile forces. But sometimes reinforcement is also used to strengthen compressed concrete (for example, in columns), as well as to withstand temperature and shrinkage stresses.
Reinforcement for reinforced concrete structures must meet the following requirements:
studfiles.net
Calculation of elastic modulus in laboratory conditions
The algorithm for determining deformation involves experimental studies in laboratory conditions using standard samples.
A standard sample is examined to establish the initial and reduced values. After conducting tests, they determine the degree of the material’s ability to withstand compression or tension. If the material does not have a reinforcement frame, then it is not capable of stretching. Taking into account the results of the experiments, a graph is constructed reflecting the indicators of the relationship between the applied impact and the destruction of the prototype.
The calculations take into account the equivalence of the elasticity of the material in tension and compression.
During laboratory research, a sample is subjected to a continuously increasing load until it is completely destroyed. The diagram contains data reflecting the impact of loads on the degree of deformation of the prototype. At the final stage, the average indicator of all studied samples is calculated.
The methodology for calculating concrete structures is contained in the Code of Rules 52-101-2003, which applies to all building concrete and reinforced concrete structures.
Modulus of elasticity of concrete: types, classification. What does it depend on
All solutions that are prone to hardening have a certain density in the frozen state, which is why there is such a thing as the elastic modulus of concrete, which determines its suitability for a particular type of work. In addition, such mixtures are also classified by brand, but the brand can include density sizes and has a more general concept.
This is exactly what will be discussed below, and you can also see a demonstration of the thematic video in this article.
Tensile test
Classification
Views and tables
Pouring a slab foundation
- All types of such solutions are divided into heavy, fine-grained, light, porous, and autoclave hardening . It is somewhat surprising that almost all home-grown builders have almost no knowledge about this, although the quality of the structure being built mainly depends on this.
- Concrete products themselves are quite hard materials, but under the influence of mechanical loads such as impact, compression, tension and fracture, even the highest modulus of elasticity of reinforced concrete cannot be quite sufficient as an absolute unit . In this regard, the classification of strength differs into two main indicators - compression and tension, on which the tolerance of other loads or elasticity depends.
Name of concrete
| Initial elastic modulus. Compression and tension Eb*10 3. Compressive strength in MPa | |||||||||||||||||||
| B1 | B1.5 | B2 | B2.5 | B3.5 | B5 | B7.5 | B10 | B12.5 | B15 | IN 20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 | |
| Heavy | |||||||||||||||||||
| Natural hardening cycle | — | — | — | 9,5 | 13 | 16 | 18 | 21 | 23 | 27 | 30 | 32,5 | 34,5 | 36 | 37,5 | 39 | 39,5 | 40 | |
| Heat treatment at atmospheric pressure | — | — | — | — | 8,5 | 11,5 | 14,5 | 16 | 19 | 20,5 | 24 | 27 | 29 | 31 | 32,5 | 34 | 35 | 35,5 | 36 |
| Autoclave processing | — | — | — | — | 7 | 10 | 12 | 13,5 | 16 | 17 | 20 | 22,5 | 24,5 | 26 | 27 | 28 | 29 | 29,5 | 30 |
| Fine-grained | |||||||||||||||||||
| A-group (natural hardening) | — | — | — | — | 7 | 10 | 13,5 | 15,5 | 17,5 | 19,5 | 22 | 24 | 26 | 27,5 | 28,5 | — | — | — | — |
| Heat treatment at atmospheric pressure | — | — | — | — | 6,5 | 9 | 12,5 | 14 | 15,5 | 17 | 20 | 21,5 | 23 | 24 | 24,5 | — | — | — | — |
| B-group (natural hardening) | — | — | — | — | 6,5 | 9 | 12,5 | 14 | 15,5 | 17 | 20 | 21,5 | 23 | — | — | — | — | — | — |
| Heat treatment under autoclave pressure | — | — | — | — | 5,5 | 8 | 11,5 | 13 | 14,5 | 15,5 | 17,5 | 19 | 20,5 | ||||||
| B-group autoclave curing | — | — | — | — | — | — | — | — | — | 16,5 | 18 | 19,5 | 21 | 21 | 22 | 23 | 24 | 24,5 | 25 |
| Light and horizontal - medium density D | |||||||||||||||||||
| 800 | — | — | — | 4 | 4,5 | 5 | 5,5 | — | — | — | — | — | — | — | — | — | — | — | — |
| 1000 | — | — | — | 5 | 5,5 | 6,3 | 7,2 | 8 | 8,4 | — | — | — | — | — | — | — | — | — | — |
| 1200 | — | — | — | 6 | 6,7 | 7,6 | 8,7 | 9,5 | 10 | 10,5 | — | — | — | — | — | — | — | — | — |
| 1400 | — | — | — | 7 | 7,8 | 8,8 | 10 | 11 | 11,7 | 12,5 | 13,5 | 14,5 | 15,5 | — | — | — | — | — | — |
| 1600 | — | — | — | — | 9 | 10 | 11,5 | 12,5 | 13,2 | 14 | 15,5 | 16,5 | 17,5 | 18 | — | — | — | — | — |
| 1800 | — | — | — | — | — | 11,2 | 13 | 14 | 14,7 | 15,5 | 17 | 18,5 | 19,5 | 20,5 | 21 | — | — | — | — |
| 2000 | — | — | — | — | — | — | 14,5 | 16 | 17 | 18 | 19,5 | 21 | 22 | 23 | 23,5 | — | — | — | — |
| Cellular, autoclave curing, density D | |||||||||||||||||||
| 500 | 1,1 | 1,4 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 600 | 1,4 | 1,7 | 1,8 | 2,1 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 700 | — | 1,9 | 2,2 | 2,5 | 2,9 | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 800 | — | — | — | 2,9 | 3,4 | 4 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 900 | — | — | — | — | 3,8 | 4,5 | 5,5 | — | — | — | — | — | — | — | — | — | — | — | — |
| 1000 | — | — | — | — | — | 6 | 7 | — | — | — | — | — | — | — | — | — | — | — | — |
| 1100 | — | — | — | — | — | 6,8 | 7,9 | 8,3 | 8,6 | — | — | — | — | — | — | — | — | — | — |
| 1200 | — | — | — | — | — | — | 8,4 | 8,8 | 9,3 | — | — | — | — | — | — | — | — | — | — |
Calculated resistances and elastic moduli of heavy concrete, mPa
table 2
| Characteristics concrete | CONCRETE CLASS | ||||||||
| B7.5 | AT 10 | B12.5 | B15 | IN 20 | B25 | B30 | B35 | B40 | |
| For limit states of the 1st group | |||||||||
| Axial compression (prismatic strength) Rb | 4,5 | 6,0 | 7,5 | 8,5 | 11,5 | 14,5 | 17,0 | 19,5 | 22,0 |
| Axial tension Rbt | 0,48 | 0,57 | 0,66 | 0,75 | 0,90 | 1,05 | 1,20 | 1,30 | 1,40 |
| For limit states of the 2nd group | |||||||||
| Axial compression Rb, ser | 5,5 | 7,5 | 9,5 | 11,0 | 15,0 | 18,5 | 22,0 | 25,5 | 29,0 |
| Axial tension Rbt, ser | 0,70 | 0,85 | 1,00 | 1,15 | 1,30 | 1,60 | 1,80 | 1,95 | 2,10 |
| Initial modulus of elasticity of heavy concrete of normal hardening Eb | 16000 | 18000 | 21000 | 23000 | 27000 | 30000 | 32500 | 34500 | 36000 |
| Initial modulus of elasticity of heavy concrete subjected to heat treatment at atmospheric pressure | 14500 | 16000 | 19000 | 20500 | 24000 | 27000 | 29000 | 31000 | 32500 |
Note. The calculated resistances of concrete for limit states of the 2nd group are equal to the standard ones: Rb,ser =Rb,n; Rbt,ser =R bt,n.
Calculated resistances and elastic moduli of some reinforcing steels, mPa
Table 3
| CLASS FITTINGS (designation according to DSTU 3760-98) | Calculated resistances | Elastic modulus Es | |||
| for calculation according to limit states of group 1 | for calculations based on limit states of the 2nd group Rs,ser | ||||
| stretching | compression Rsc | ||||
| Rs | Rsw | ||||
| 1 А240С | 2 | 3 | 4 | 5 | 6 |
| 225 | 175 | 225 | 235 | 2,1·105 | |
| А300С | 280 | 225 | 280 | 295 | 2,1·105 |
| А400С 6…8 mm | 355 | 285 | 355 | 390 | 2,0·105 |
| А400С 10…40mm | 365 | 290 | 365 | 365 | 2,0·105 |
| А600С | 510 | 405 | 450 | 590 | 1,9·105 |
| BpI 3 mm | 375 | 270 | 375 | 410 | 1,7·105 |
| BpI 4 mm | 365 | 265 | 365 | 405 | 1,7·105 |
| BpI 5 mm | 360 | 260 | 360 | 395 | 1,7·105 |
Note. The calculated steel resistances for limit states of the 2nd group are equal to the standard ones: Rs,ser =Rs,n.
studfiles.net
What does the elasticity of concrete depend on?
1. Composition
Concrete with a higher elastic modulus undergoes less relative deformation.
A significant role in this is played by the quality of cement stone and filler - the two components that make up concrete. Both the solution and the aggregate take on the entire load. When analyzing the dependence of the modulus of elasticity of concrete on the modulus of elasticity of its components, researchers found that the strength of the aggregate is not always used to improve the characteristics of the finished material, but the elasticity index has a significant impact.
2. Class
The initial modulus of elasticity of concrete during compression and expansion depends on the class of the product in terms of compressive strength.
This dependence is established by applying empirical formulas, so for practical purposes it is easiest to obtain information from a ready-made table. Even without complex mathematical calculations, you can see that the elastic modulus increases in proportion to the strength of the material. In other words, the higher the class, the greater the modulus of elasticity of concrete, i.e. material of class B25 is more resistant to relative deformations compared to B20.
Modulus of elasticity of concrete in tension and compression
This concept is known mainly to specialists. For an “amateur” builder, a private developer, this phrase means little. But the durability of a particular building directly depends on it.
Concrete itself is a hard material. And, nevertheless, under the influence of various external forces it is partially deformed. That is why there are two indicators of its strength - tensile and compressive, although they focus more on the latter. Consequently, the elastic moduli must also be designed accordingly for these diverse influences.
But in practice, they are accepted as equal and indicate the ability of concrete to temporarily deform under the influence of increased loads, without undergoing irreversible changes - destruction of the structure, the appearance of cracks, chips, and the like. This is especially important to know when the structure is subject to various deflections (for example, arch-type reinforced concrete structures, floors). Unlike many other building materials, concrete under the influence of load (within certain limits) acts like a spring.
The indicator under consideration is determined experimentally based on testing samples of materials. It is designated by the symbol “E” and has a second name – “Young’s modulus”. There are initial and reduced modulus of elasticity (Eb and Eb1, respectively). For the average user, all these calculations and the formulas used are of no practical importance, since only a specialized specialist can understand all the nuances.
You just need to know what influences this characteristic of the material, as well as the existence of tables that can be used if necessary.
What does the modulus of elasticity depend on?
1. The characteristics of the filler have a direct influence, and this dependence is almost linear (if displayed graphically). For lightweight concrete, the modulus value is lower than the same indicator for “heavy” analogues with large granules (crushed stone, gravel).
2. Concrete class. There is a special table for the definition. In practice, a private developer uses a limited range of such products, so there is no point in presenting them in full. Here are some data on strength and modulus, from which it is clear that they have a directly proportional relationship, which does not change at temperatures up to 230 0C. Therefore, almost never.
- B10 corresponds to 19;
- At 15 – 24;
- B20 – 27.5;
- B25 – 30;
- B30 – 32.5.
This allows you to “control” such a material property as elasticity, and for the same brand of product. This characteristic is taken into account depending on which structural element will be installed. For example, lightly or heavily loaded, with what frequency and duration will the additional weight be applied.
3. Age of concrete. There is a tendency for the numerical indicator of the elastic modulus to increase over time. Therefore, when determining the value for a specific period, special tables are used, which reflect the initial indicators, which are multiplied by correction factors.
4. Materials processing technology. There is a difference in how the concrete hardened - naturally, during heat treatment without the use of closed chambers, or “passed” through an autoclave.
5. Duration of load exposure. To determine this value, the initial elastic modulus (taken from the table) is multiplied by the corresponding coefficient. It is equal to 0.85 for fine-grained, light (if the aggregate is small) and heavy concrete. For lightweight (with porous aggregate) and porous concrete, the coefficient is 0.7.
Before considering other factors that influence the characteristic under consideration, it is worth focusing on such an indicator as the creep of concrete. The degree of deformation of the material depends on it. The fact is that with short-term exposure (and within certain limits) after the load is removed, the material takes on its original shape.
If the impact does not stop, then we are talking about plastic deformation, which, as a rule, is irreversible. You should not go into all the nuances, since sometimes it is extremely difficult to separate both types of deformation. It is enough to point out that plasticity (that is, a further change in shape) is caused by the “creep” of concrete. It is taken into account for long-term exposure. The creep coefficient is indicated by the symbol “φb,cr”
6. Air humidity. There is a relationship between it and φb,cr. This is also determined from the tables. In addition, factors such as temperature and radiation (radiation intensity) are also taken into account.
7. Presence of a reinforcing frame. It is clear that metal does not deform under load to the same extent as concrete.
For those readers who want to delve deeper into this issue, we point out State Standard No. 24452 of 1980, which describes, in particular, methods for determining this characteristic of concrete.
aquagroup.ru